Exponential smoothing
Mean
\hat y_{T+1\mid T}=\tfrac{1}{T}\sum_{i=1}^T y_i
Naïve
\hat y_{T+1\mid T}=y_T
Mean
Naïve
Exponential Smoothing
\hat y_{T+1\mid T}=\alpha y_T + \alpha(1-\alpha)y_{T-1} + \ldots
\alpha \approx 1: naïve-like
\alpha \approx 0: mean-like
\hat{y}_{T+1 | T}= \alpha y_{T} + \alpha(1-\alpha) y_{T-1} + \alpha(1-\alpha)^{2} y_{T-2} + \ldots
where 0\leq \alpha \leq1 is the smoothing parameter.
| \alpha = 0.2 | \alpha = 0.4 | \alpha = 0.6 | \alpha = 0.8 | |
|---|---|---|---|---|
| y_t | 0.2000 | 0.4000 | 0.6000 | 0.8000 |
| y_{t-1} | 0.1600 | 0.2400 | 0.2400 | 0.1600 |
| y_{t-2} | 0.1280 | 0.1440 | 0.0960 | 0.0320 |
| y_{t-3} | 0.1024 | 0.0864 | 0.0384 | 0.0064 |
| y_{t-4} | 0.0819 | 0.0518 | 0.0154 | 0.0013 |
| y_{t-5} | 0.0655 | 0.0311 | 0.0061 | 0.0003 |
Exponential smoothing methods
Simple exponential smoothing (SES)
\begin{aligned} \text{Forecast equation} \quad & \hat{y}_{t+h|t} = \ell_t \\ \text{Smoothing equation} \quad & \ell_t = \alpha y_t + (1-\alpha)\ell_{t-1} \end{aligned}
where \ell_t is the level at time t.
SES has a flat forecast function, so it is appropriate for data with no trend or seasonal pattern.
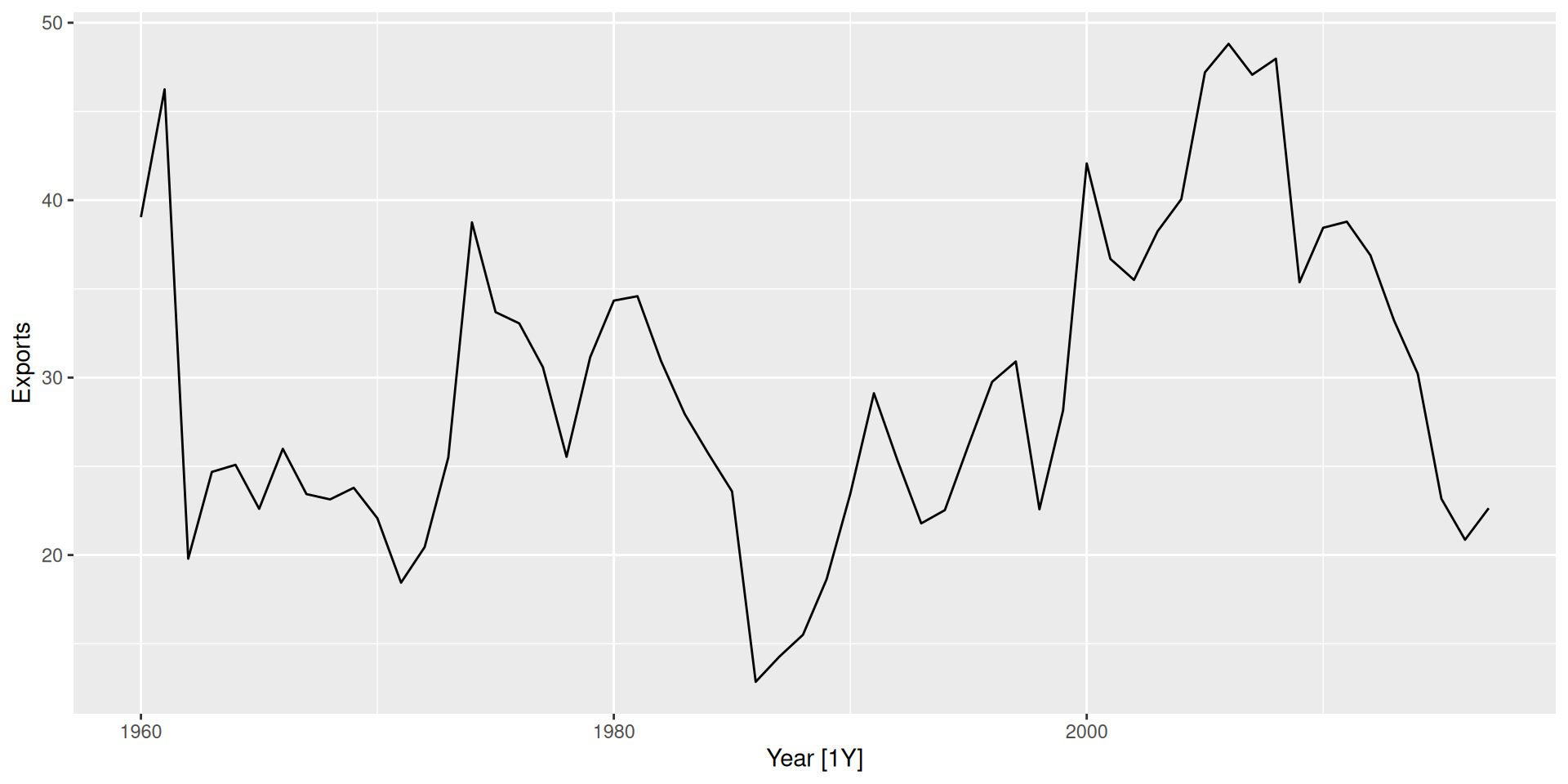
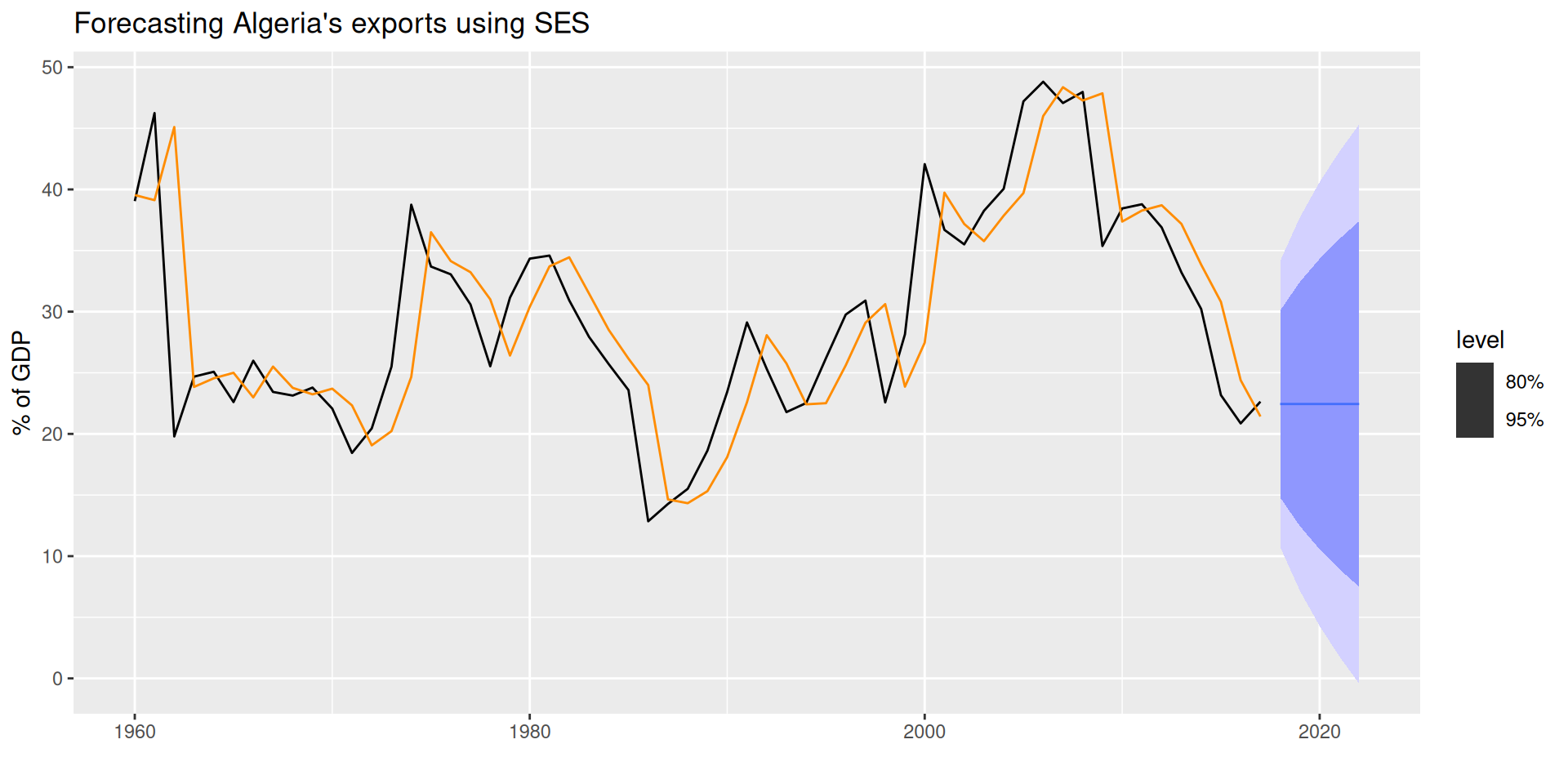
Example: Forecasting Algeria’s exports
- 1
-
We specify
trend("N")andseason("N")to indicate that we want a simple exponential smoothing (SES) model, which assumes no trend and no seasonality. The model will estimate the smoothing parameter \alpha automatically.
Obtaining the report() of a model
- 1
-
The
report()function allows us to see a model’s report (the time series modeled, the model used, the estimated parameters, and more). It needs a 1 \times 1 dimensionmable1.
Series: Exports
Model: ETS(A,N,N)
Smoothing parameters:
alpha = 0.8399875
Initial states:
l[0]
39.539
sigma^2: 35.6301
AIC AICc BIC
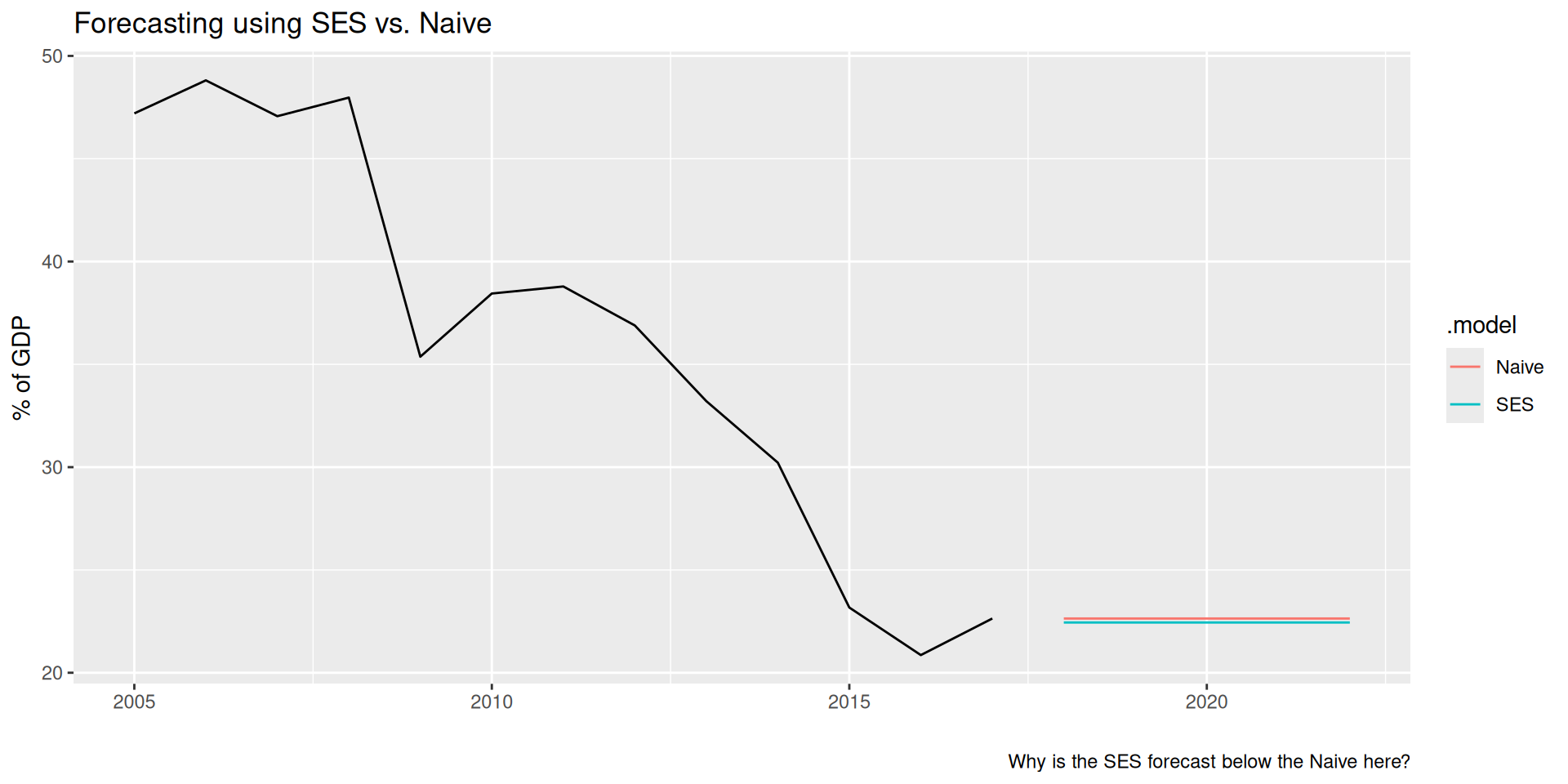
446.7154 447.1599 452.8968 Comparing the SES and Naive forecasts:
Methods with trend
Holt’s linear trend
\begin{aligned} \text{Forecast equation} \quad & \hat{y}_{t+h|t} = \ell_t + hb_t \\ \text{Level equation} \quad & \ell_t = \alpha y_t + (1-\alpha)\ell_{t-1}\\ \text{Trend equation} \quad & b_t = \beta^*(\ell_t - \ell_{t-1}) + (1-\beta^*)b_{t-1} \end{aligned}
where b_t is the growth (or slope) at time t.
When to use Holt’s linear trend method
- Holt’s linear trend method is appropriate for data with a linear trend but no seasonal pattern.
- The proper benchmark method to compare against is the drift method.
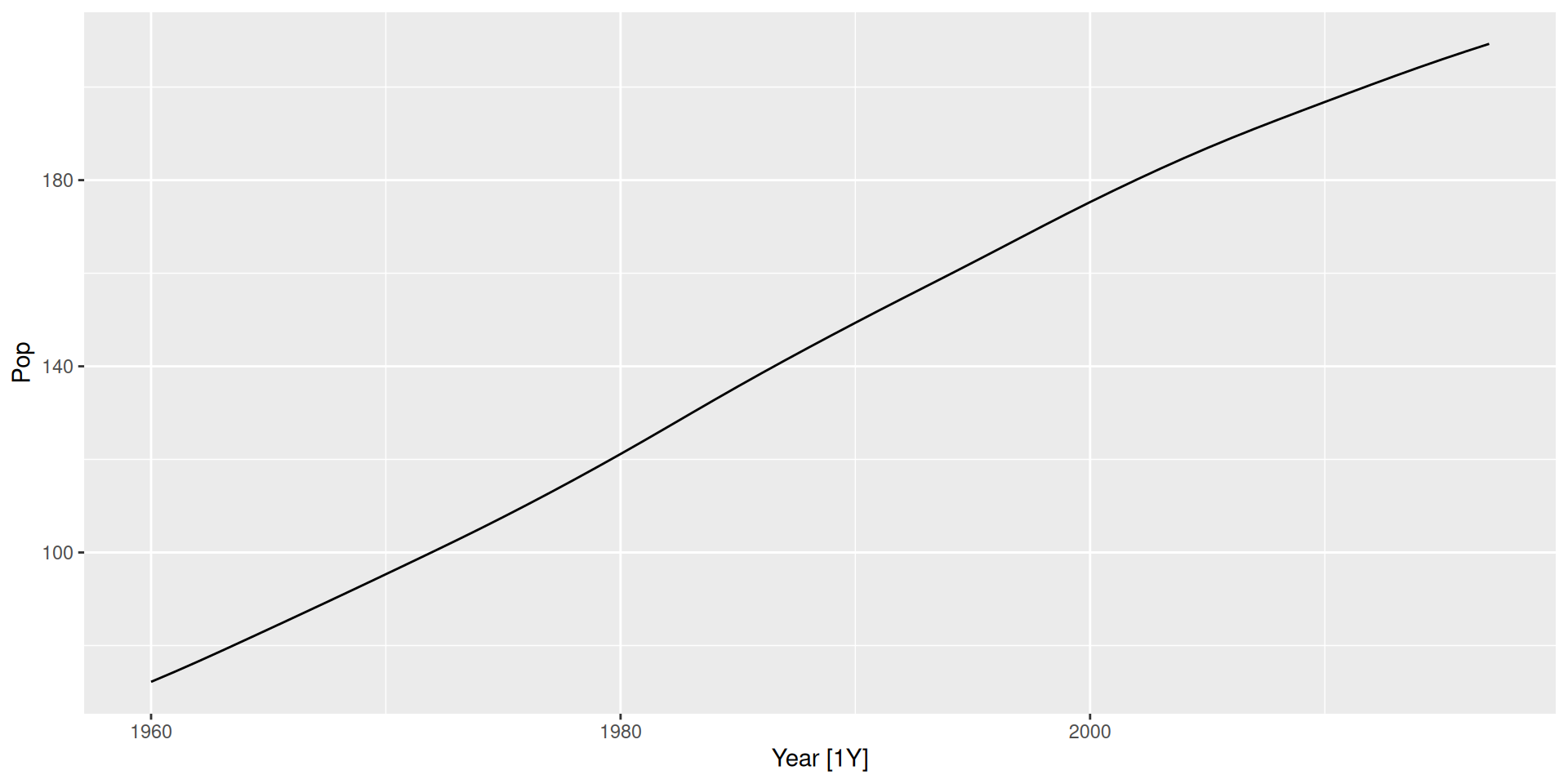
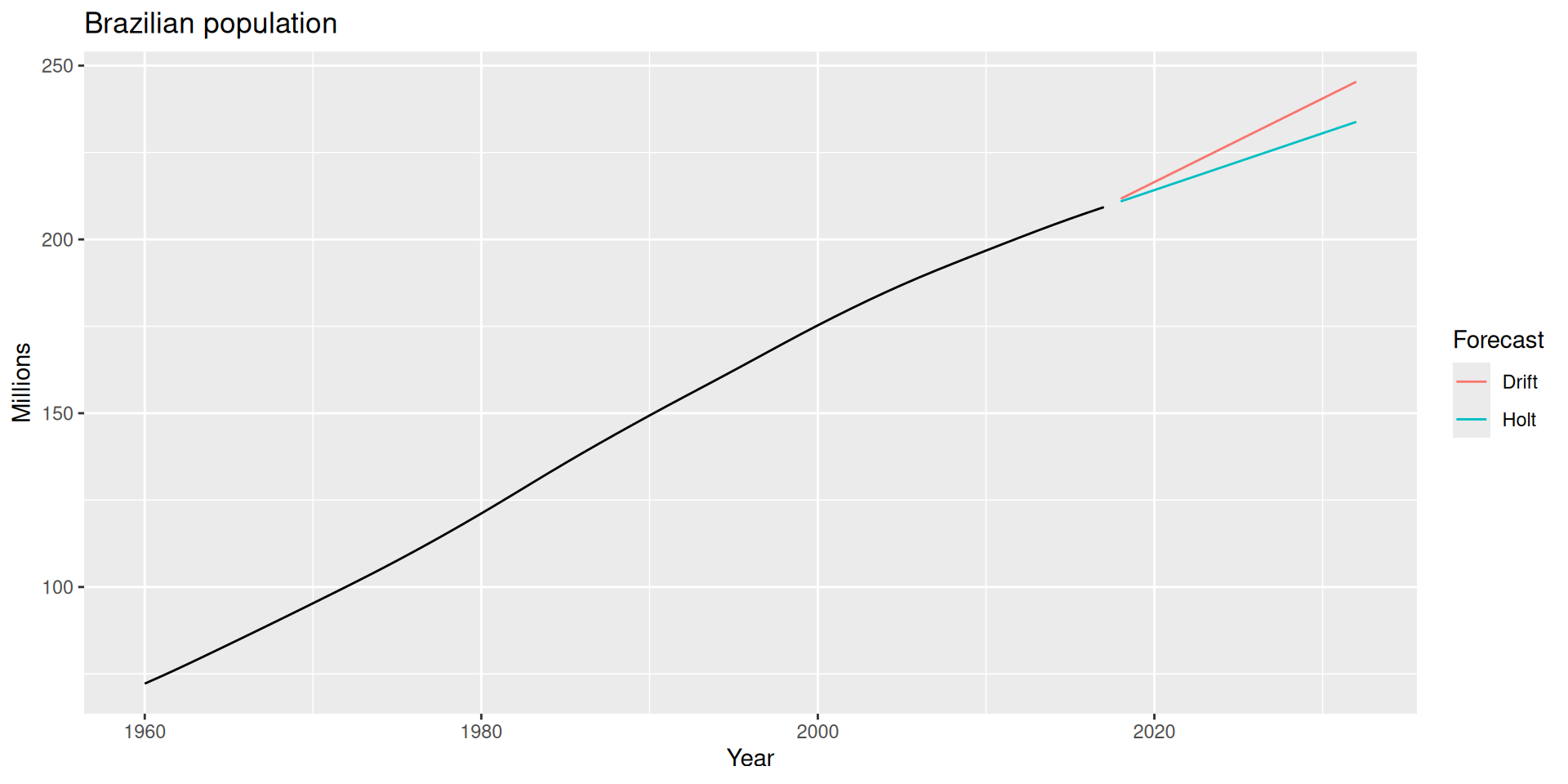
Example: Forecasting Brazil’s population
Example: Forecasting Brazil’s population
Example: Forecasting Brazil’s population
Example: Forecasting Brazil’s population
Series: Pop
Model: ETS(A,A,N)
Smoothing parameters:
alpha = 0.9999
beta = 0.9998999
Initial states:
l[0] b[0]
70.06297 2.132884
sigma^2: 0.0021
AIC AICc BIC
-115.2553 -114.1014 -104.9531 Example: Forecasting Brazil’s population
bra_fit <- bra_economy |>
model(
Holt = ETS(Pop ~ error("A") + trend("A") + season("N")),
Drift = RW(Pop ~ drift())
)
bra_fit |>
select(Holt) |>
report()
bra_fc <- bra_fit |>
forecast(h = 15)
bra_fc |>
autoplot(bra_economy, level = NULL) +
labs(title = "Brazilian population",
y = "Millions") +
guides(colour = guide_legend(title = "Forecast"))- 1
-
We specify
trend("A")to indicate that we want a linear trend. The model will estimate the smoothing parameters \alpha and \beta^* automatically.
Series: Pop
Model: ETS(A,A,N)
Smoothing parameters:
alpha = 0.9999
beta = 0.9998999
Initial states:
l[0] b[0]
70.06297 2.132884
sigma^2: 0.0021
AIC AICc BIC
-115.2553 -114.1014 -104.9531 Damped trend
\begin{aligned} \text{Forecast equation} \quad & \hat{y}_{t+h|t} = \ell_t + (\phi + \phi^2 + \ldots + \phi^h) b_t \\ \text{Level equation} \quad & \ell_t = \alpha y_t + (1 - \alpha) (\ell_{t-1} + \phi b_{t-1}) \\ \text{Trend equation} \quad & b_t = \beta^*(\ell_t-\ell_{t-1}) + (1-\beta^*)\phi b_{t-1} \end{aligned}
where 0 < \phi < 12 is the damping parameter.
What would happen if \phi = 1? What about if \phi = 0?
- If \phi = 1, the model reduces to Holt’s linear trend method, meaning the trend continues indefinitely at the same rate.
- If \phi = 0, the trend component is completely eliminated, and the model behaves like simple exponential smoothing (SES), where forecasts are based solely on the level component without any trend influence.
Example: Forecasting Brazil’s population (continued)
Example: Forecasting Brazil’s population (continued)
Example: Forecasting Brazil’s population (continued)
bra_economy |>
model(
Holt = ETS(Pop ~ error("A") + trend("A") + season("N")),
Damped = ETS(Pop ~ error("A") + trend("Ad", phi = 0.9) + season("N"))
) |>
forecast(h = 15) |>
autoplot(bra_economy, level = NULL) +
labs(title = "Brazilian population",
y = "Millions") +
guides(colour = guide_legend(title = "Forecast"))- 1
-
We specify
trend("Ad")to indicate that we want a damped trend, andphi = 0.9sets the damping parameter to 0.9. We could also let the model estimate \phi automatically by omitting thephiargument.
Methods with seasonality
Holt-Winters method
HW - Additive
\begin{aligned} \text{Forecast equation} \quad & \hat{y}_{t+h|t} = \ell_t + hb_t + s_{t+h-m(k+1)} \\ \text{Level equation} \quad & \ell_t = \alpha (y_t - s_{t-m}) + (1 - \alpha) (\ell_{t-1} + b_{t-1}) \\ \text{Trend equation} \quad & b_t = \beta^*(\ell_t-\ell_{t-1}) + (1-\beta^*) b_{t-1} \\ \text{Seasonal equation} \quad & s_t = \gamma(y_t - \ell_{t-1} - b_{t-1}) + (1-\gamma)s_{t-m} \end{aligned}
where s_t is the seasonal component at time t, m is the period of the seasonality3, and k = \lfloor (h-1)/m \rfloor.
HW - Multiplicative
\begin{aligned} \text{Forecast equation} \quad & \hat{y}_{t+h|t} = (\ell_t + hb_t) s_{t+h-m(k+1)} \\ \text{Level equation} \quad & \ell_t = \alpha \frac{y_t}{s_{t-m}} + (1 - \alpha)(\ell_{t-1} + b_{t-1}) \\ \text{Trend equation} \quad & b_t = \beta^*(\ell_t-\ell_{t-1}) + (1-\beta^*) b_{t-1} \\ \text{Seasonal equation} \quad & s_t = \gamma \frac{y_t}{\ell_{t-1} + b_{t-1}} + (1-\gamma)s_{t-m} \end{aligned}
When to use Holt-Winters methods
- Holt-Winters methods are appropriate for data with a trend and seasonal pattern.
- Use an additive model when the seasonal fluctuations are roughly constant over time.
- Use a multiplicative model when the seasonal variation increase or decrease over time.
- The proper benchmark method to compare against is the seasonal naïve method. for seasonal data.
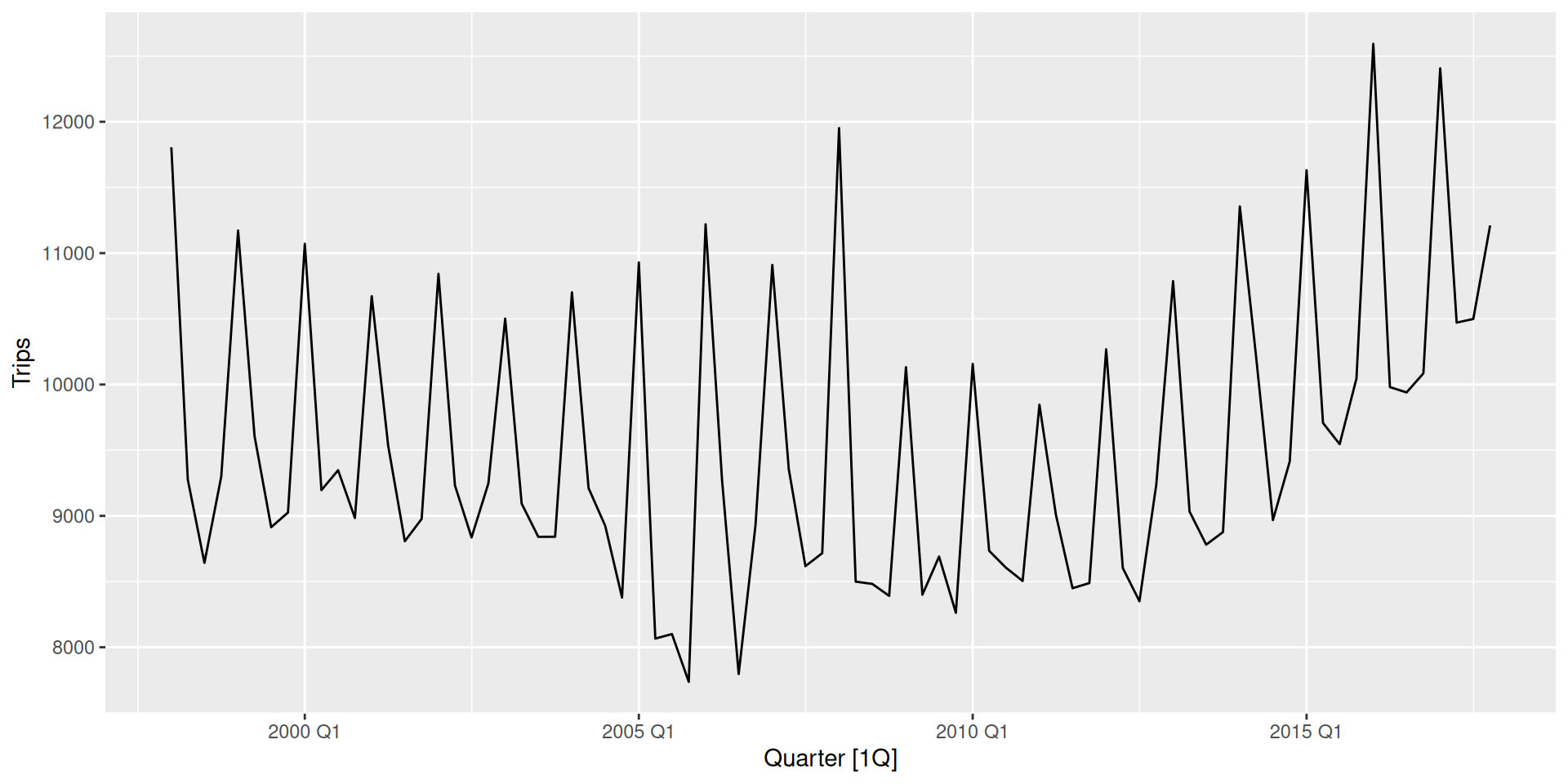
Example: Forecasting Australian holiday trips
Example: Forecasting Australian holiday trips
Example: Forecasting Australian holiday trips
Example: Forecasting Australian holiday trips
Example: Forecasting Australian holiday trips
The tidy() function for models
- 1
-
The
tidy()function allows us to see the estimated parameters of each model in a tidy table.
Example: Forecasting Australian holiday trips
aus_fc |>
autoplot(aus_holidays, level = NULL) + xlab("Year") +
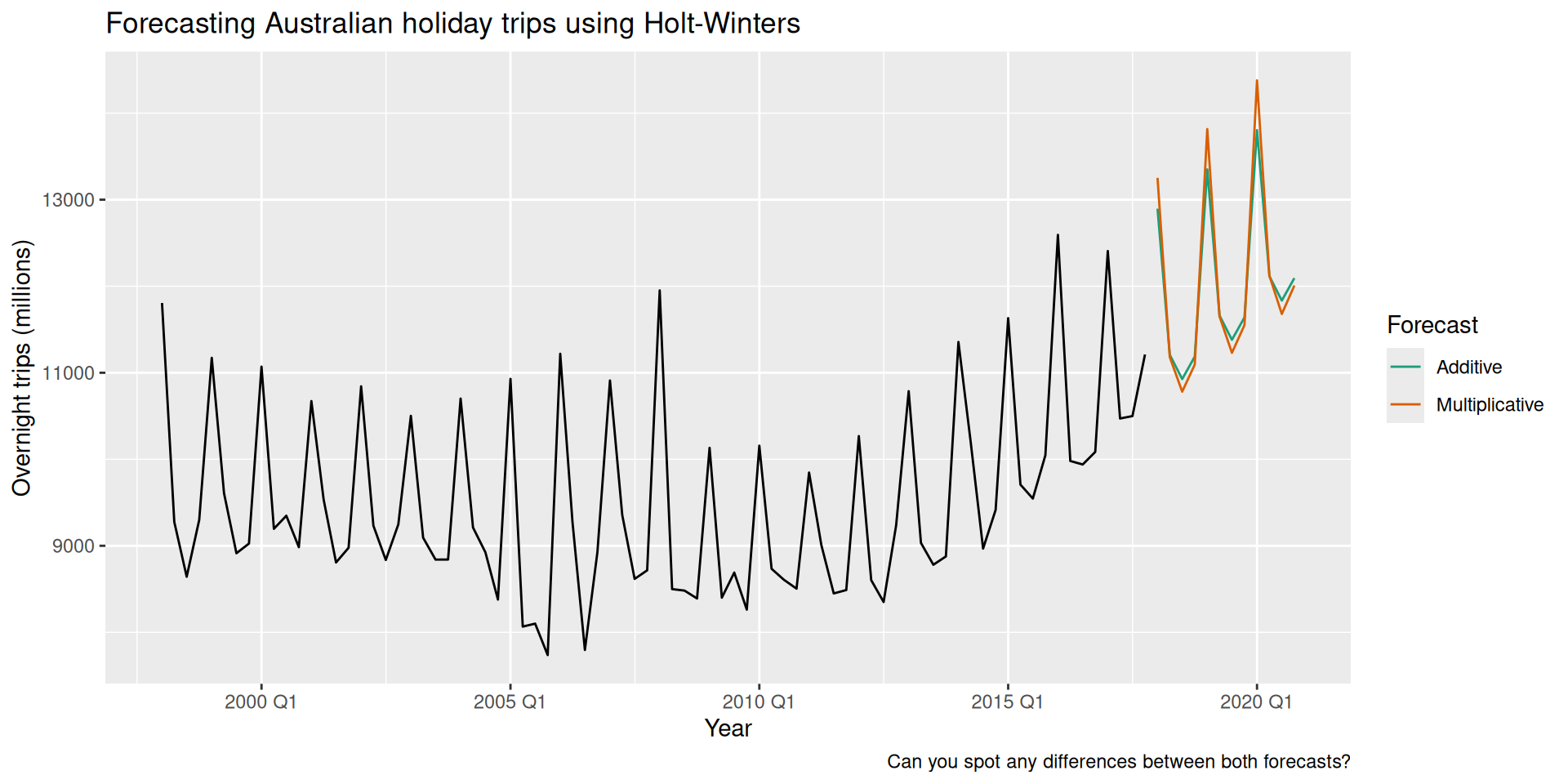
labs(
title = "Forecasting Australian holiday trips using Holt-Winters",
y = "Overnight trips (millions)",
caption = "Can you spot any differences between both forecasts?"
) +
scale_color_brewer(type = "qual", palette = "Dark2") +
guides(colour = guide_legend(title = "Forecast"))Holt-Winters’ damped method
\begin{aligned} \text{Forecast equation} \quad & \hat{y}_{t+h|t} = [\ell_t +(\phi + \phi^2 + \ldots + \phi^h)b_t] s_{t+h-m(k+1)} \\ \text{Level equation} \quad & \ell_t = \alpha \frac{y_t}{s_{t-m}} + (1 - \alpha)(\ell_{t-1} + b_{t-1}) \\ \text{Trend equation} \quad & b_t = \beta^*(\ell_t-\ell_{t-1}) + (1-\beta^*) \phi b_{t-1} \\ \text{Seasonal equation} \quad & s_t = \gamma \frac{y_t}{\ell_{t-1} + \phi b_{t-1}} + (1-\gamma)s_{t-m} \end{aligned}
Example: Forecasting daily pedestrian traffic
sth_cross_ped <- pedestrian |>
filter(Date >= "2016-07-01",
Sensor == "Southern Cross Station") |>
index_by(Date) |>
summarise(Count = sum(Count)/1000)
sth_cross_ped |>
filter(Date <= "2016-07-31") |>
model(
hw = ETS(Count ~ error("M") + trend("Ad") + season("M"))
) |>
forecast(h = "2 weeks") |>
autoplot(sth_cross_ped |> filter(Date <= "2016-08-14")) +
labs(title = "Daily traffic: Southern Cross",
y="Pedestrians ('000)")The setup ETS(y ~ error("M") + trend("Ad") + season("M")) is often a robust choice for seasonal data with trend.
Automatic ETS selection
Example: Forecasting daily pedestrian traffic (continued)
The lineup of exponential smoothing methods
| Trend component | N (None) | A (Additive) | M (Multiplicative) |
|---|---|---|---|
| N (None) | (N,N), | (N,A) | (N,M) |
| A (Additive) | (A,N), | (A,A) | (A,M) |
| A_d (Additive damped) | (A_d,N), | (A_d, A) | (A_d,M) |
| Notation | Method |
|---|---|
| (N,N) | Simple Exponential Smoothing (SES) |
| (A,N) | Holt’s Linear Trend |
| (A_d,N) | Additive damped Trend |
| (A,A) | Holt-Winters’ Additive |
| (A,M) | Holt-Winters’ Multiplicative |
| (A_d,M) | Holt-Winters’ damped |
In summary
- Exponential smoothing methods are a family of forecasting methods that use weighted averages of past observations to make forecasts.
- The weights decrease exponentially for older observations, controlled by smoothing parameters.
- Different configurations of ETS models can be used to handle various data patterns, including trend and seasonality.
- The choice of model components (
error(c("A", "M")),trend(c("N", "A", "Ad")),seasonality(c("N", "A", "M"))) should be based on the characteristics of the data.- That is, we choose the model by viewing the time plot.
- Automatic ETS selection can be a powerful tool for fitting models to multiple time series efficiently.
Footnotes
(i.e., a
mablecontaining only one model and one time series.)In practice, we restrict 0.8 \leq \phi \leq 0.98 because the damping effect would be too great for smaller values than 0.8 and almost non distinguishable from a linear trend for greater values than 0.98.
e.g., m=4 for quarterly data, m=12 for monthly data, …
as the decomposition method
for the seasonally adjusted series
for the seasonal component

Time Series Forecasting